< G4double pX,
< G4double pY,
< G4double pZ)
<
pX = 30, pY < = 40, pZ = 60
<
| G4Box(const G4String& pName, < G4double pX, < G4double pY, < G4double pZ) < pX = 30, pY < = 40, pZ = 60 |
<
<  |
<
G4Box* aBox = new G4Box("BoxA", 1.0*cm, 3.0*cm, 5.0*cm);
---
>
> G4Box* aBox = new G4Box("BoxA", 1.0*cm, 3.0*cm, 5.0*cm);
140,157c128,136
<
<
| G4Tubs(const G4String& pName, < G4double pRMin, < G4double pRMax, < G4double pDz, < G4double pSPhi, < G4double pDPhi) < < pRMin = 10, pRMax = 15, pDz = 20 |
<
<  |
<
< giving its name pName and s parameters which are --- >
> G4Tubs(const G4String& pName, > G4double pRMin, > G4double pRMax, > G4double pDz, > G4double pSPhi, > G4double pDPhi) >> giving its name pName and its parameters which are 168c147 <
<
| G4Cons(const G4String& pName, < < G4double pRmin1, < < < G4double pRmax1, < G4double pRmin2, < G4double pRmax2, < G4double pDz, < < G4double pSPhi, < G4double pDPhi)
< pRmin1 = 5, pRmax1 = 10, pRmin2 = 20, pRmax2 = 25 |
<
<  |
<
<
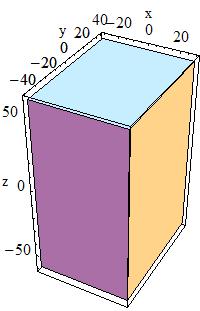
| G4Para(const G4String& pName, < G4double dx, < < G4double dy, < < G4double dz, < G4double alpha, < G4double theta, < < G4double phi ) dx = 30, dy = 40, dz = 60 |
<
<  |
<
<
| G4Trd( const G4String& pName, < G4double dx1, < < G4double dx2, < G4double dy1, < < G4double dy2, < G4double dz )
< dx1 = 30, dx2 = 10 |
<
< 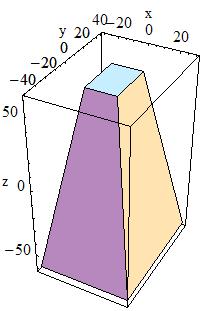 |
<
<
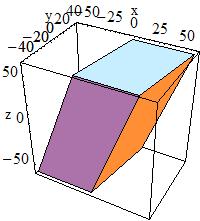
| G4Trap( const G4String& pName, < G4double pZ, < < G4double pY, < < G4double pX, < G4double pLTX )
< G4Trap( const G4String& pName,
< pDx1 = 30, pDx2 = 40, pDy1 = 40 |
<
< 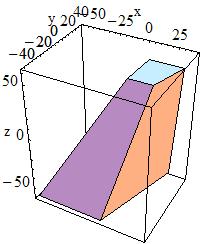 |
<
or to obtain the general trapezoid (see the Software Reference Manual):
<| pDx1 | Half x length at y=-pDy < |
| pDx2 | Half x length at y=+pDy < |
| pDy | Half y length < |
| pDz | Half z length < |
| pTheta | Polar angle of the line joining the centres of the faces at -/+pDz < |
| pDy1 | Half y length at -pDz < |
| pDx1 | Half x length at -pDz, y=-pDy1 < |
| pDx2 | Half x length at -pDz, y=+pDy1 < |
| pDy2 | Half y length at +pDz < |
| pDx3 | Half x length at +pDz, y=-pDy2 < |
| pDx4 | Half x length at +pDz, y=+pDy2 < |
| pAlph1 | Angle with respect to the y axis from the centre of the side < (lower endcap) |
| pAlph2 | Angle with respect to the y axis from the centre of the side < (upper endcap) |
<
< To build a sphere use: --- > For the complete set of constructors see the Software Reference Manual.
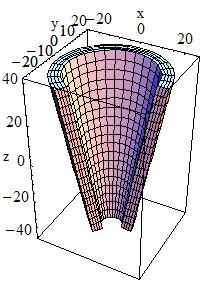
370,387c242,248 <| G4Sphere( const G4String& pName, < G4double pRmin, < < G4double pRmax, < G4double pSPhi, < < G4double pDPhi, < G4double pSTheta, < < G4double pDTheta ) pRmin = 100, pRmax = 120 |
<
< 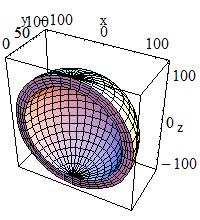 |
<
--- > To build a sphere use: >
> G4Sphere( const G4String& pName, > G4double pRmin, G4double pRmax, > G4double pSPhi, G4double pDPhi, > G4double pSTheta, G4double pDTheta ) >403,420c264 < <
To build a full solid sphere use:
<| G4Orb(const G4String& pName, G4double pRmax) < pRmax = 100 |
<
< 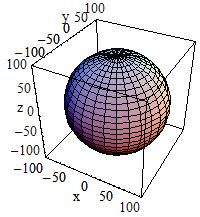 |
<
The Orb is can be obtained from a Sphere with pRmin= 0, pSPhi < = 0, pDPhi = 2 Pi, pSTheta = 0, pDTheta = Pi.
<| pRmax | Outer radius < |
< --- > 423,434d266 <
<
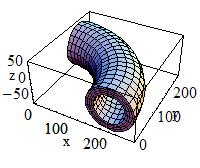
| G4Torus( const G4String& pName, < G4double pRmin, G4double pRmax, < G4double pRtor, G4double pSPhi, G4double pDPhi )
< pRmin = 40, pRmax = 60, pRtor = 200 |
<
<  |
<
<
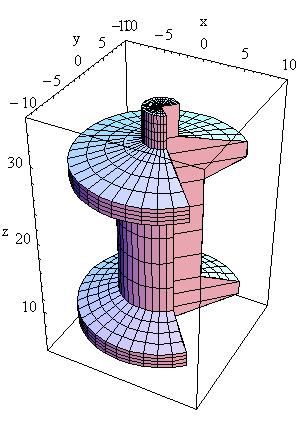
| G4Polycone( const G4String& pName, < G4double phiStart, < G4double phiTotal, < G4int numZPlanes, < const G4double zPlane[], < < const G4double rInner[], < const G4double rOuter[]) < < G4Polycone( const G4String& pName, < G4double phiStart, < G4double phiTotal, < G4int numRZ, < const G4double r[], < const G4double z[])
< phiStart = 0*Degree, phiTotal = 2*Pi |
<
<  |
<
< <
| G4Polyhedra( const G4String& pName, < G4double phiStart, < G4double phiTotal, < G4int numSide, < G4int numZPlanes, < const G4double zPlane[], < const G4double rInner[], < const G4double rOuter[] ) < < G4Polyhedra( const G4String& pName, < G4double phiStart, < G4double phiTotal, < G4int numSide, < G4int numRZ, < const G4double r[], < const G4double z[] )
< phiStart = 0, phiTotal= 2 Pi |
<
<  |
<
<
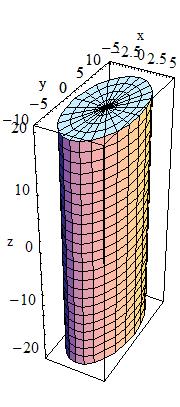
| G4EllipticalTube( const G4String& pName,
< < G4double Dx, < G4double Dy, < G4double Dz ) < Dx = 5, Dy = 10, Dz = 20 |
<
<  |
<
| Dz | Half length in Z < |
<
The general ellipsoid can be defined as follows:
<< <
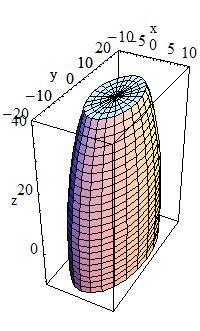
| G4Ellipsoid(const G4String& pName, < G4double < pxSemiAxis, < < G4double pySemiAxis, < < G4double pzSemiAxis, < < G4double pzBottomCut=0, < < G4double pzTopCut=0); < pxSemiAxis = 10, pySemiAxis = 20, pzSemiAxis = 50 |
<
<  |
<
A general (or triaxial) ellipsoid is a quadratic surface which is given in < Cartesian coordinates by
<1.0 = (x/pxSemiAxis)**2 + (y/pySemiAxis)**2 + (z/pzSemiAxis)**2
<| pxSemiAxis | Semiaxis in X < |
| pySemiAxis | Semiaxis in Y < |
| pzSemiAxis | Semiaxis in Z < |
| pzBottomCut | lower cut plane level, z |
| pzTopCut | upper cut plane level, z < |
< A cone with an elliptical cross section can be defined as follows:
<
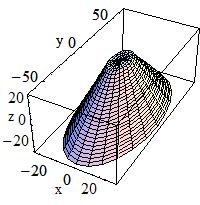
| G4EllipticalCone(const G4String& pName, < < G4double pxSemiAxis, < < G4double pySemiAxis, < < G4double zMax, < < G4double pzTopCut); < pxSemiAxis = 0.5, pySemiAxis = 1 |
<
<  |
<
<
| pxSemiAxis | Semiaxis in X < |
| pySemiAxis | Semiaxis in Y < |
| zMax | Height of elliptical cone |
| pzTopCut | upper cut plane level |
< An elliptical cone of height zMax, semiaxis pxSemiAxis, and semiaxis pySemiAxis < is given by the parametric equations
< x = pxSemiAxis * ( zMax - u ) / u * Cos v
< y = pySemiAxis * ( zMax - u ) / u * Sin v
< z = u <
< Where v is between 0 and 2 Pi, and u between 0 and h respectively. --- >
678,692d397 <
<
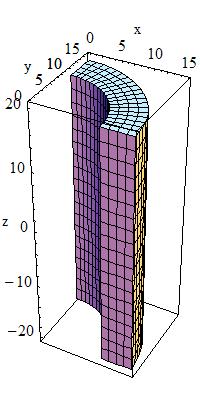
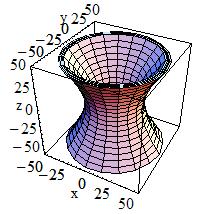
| G4Hype(const G4String& pName, < G4double innerRadius, < G4double outerRadius, < G4double innerStereo, < G4double outerStereo, < G4double halfLenZ )
< innerStereo = 0.7, outerStereo = 0.7 |
<
<  |
<
<
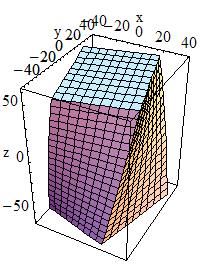
| G4TwistedBox(const G4String& pName, < G4double twistedangle, < G4double pDx, < G4double pDy, < G4double pDz)
< twistedangle = 30*Degree |
<
<  |
<
<
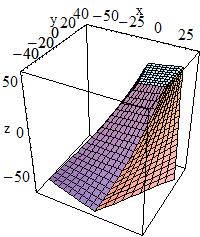
| G4TwistedTrap(const G4String& pName, < G4double twistedangle, < G4double pDxx1, < G4double pDxx2, < G4double pDy, < G4double pDz) < < G4TwistedTrap(const G4String& pName, < G4double twistedangle, < G4double pDz, < G4double pTheta, < G4double pPhi, < G4double pDy1, < G4double pDx1, < G4double pDx2, < G4double pDy2, < G4double pDx3, < G4double pDx4, < G4double pAlph)
< pDx1 = 30, pDx2 = 40, pDy1 = 40 |
<
<  |
<
<
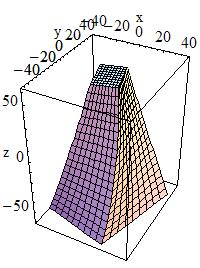
| G4TwistedTrd(const G4String& pName, < G4double pDx1, < G4double pDx2, < G4double pDy1, < G4double pDy2, < G4double pDz, < G4double twistedangle)
< dx1 = 30, dx2 = 10 |
<
<  |
<
<
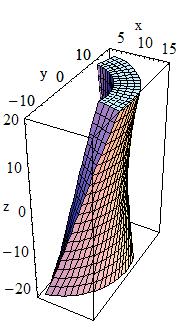
| G4TwistedTubs(const G4String& pName, < G4double twistedangle, < G4double endinnerrad, < G4double endouterrad, < G4double halfzlen, < G4double dphi)
< endinnerrad = 10, endouterrad = 15 <
|
<
<  |
<
< <
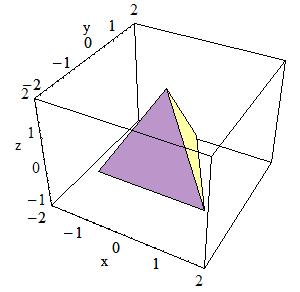
A tetrahedra solid can be defined as follows:
<| G4Tet(const G4String& pName, < < G4ThreeVector anchor, < < G4ThreeVector p2, < < G4ThreeVector p3, < < G4ThreeVector p4, < < G4bool *degeneracyFlag=0) anchor = {0, 0, sqrt(3)} |
<
<  |
<
The solid is defined by four points in space.
<| anchor | Anchor point < |
| p2 | Point 2 < |
| p3 | Point 3 |
| p4 | Point 4 |
| degeneracyFlag | Flag indicating degeneracy of points |